区块链网络中矿池选择的演化博弈
区块链网络中矿池选择的演化博弈
论文原文链接: Evolutionary Game for Mining Pool Selection in Blockchain Networks
Abstract
在基于工作量证明(POW)的区块链网络中,区块矿工参与解决加密难题的竞赛,以赢得发布(即挖掘)新区块的奖励。由于加密难题的显著难度,个体矿工倾向于加入矿池以确保稳定的利润。我们研究了区块链网络中矿池选择的动态,其中矿池可以选择任意块挖掘策略(补充)。我们将解谜的哈希率和区块传播延迟确定为决定挖矿竞争结果的两个主要因素。然后我们将个体矿工的策略演化建模为演化博弈。我们提供了两个池情况下池选择动力学中演化稳定性的理论分析。数值模拟支持我们的理论发现,并证明了一般情况下矿工策略演变的稳定性
Section1-Introduction
公共区块链网络构建为覆盖点对点 (P2P) 网络,用于去中心化防篡改数据记录。中本聪共识协议 用于在利益角度上激励全节点(区块矿工)遵守区块链状态维护的“最长链规则”。遵循该协议,区块矿工将一组任意经过验证的交易打包成一个数据结构,称为候选“区块”,并将其广播到整个网络。区块链状态被维护为由散列指针以松散同步的方式链接的块的线性列表。即,矿工始终将观察到的最长链作为其本地区块链副本。
中本聪协议的激励机制由两部分组成:
- 一个计算密集型的加密难题解决过程
- 一个奖励确认过程,用于在矿工发布的区块被网络认可时向矿工提供奖励
密码谜题解决过程是通过工作量证明 (PoW) 竞赛实现的,其中矿工详尽地查询可信随机预言机,例如 SHA-256 哈希函数,以找到满足原像的随机字符串条件基于他们自己的区块提议。在奖励过程中,首先在网络上传播其候选区块的矿工因其在验证新交易方面的努力而获得数字代币奖励。与移动网络中流行的激励机制相比,中本聪协议的特点是在其区块确认功能中嵌入了去中心化的代币发行方案。在每个区块固定奖励的情况下,节点加入共识过程的意愿主要受能源消耗预期成本的影响。
赢得 PoW 竞赛的概率取决于矿工的哈希率(即矿工每秒对哈希函数的查询次数)与整个网络的总哈希率之间的比率。同时,P2P网络中的区块传播时间决定了一个共识回合内区块确认的最终结果,因为只有传播到大多数节点的第一个区块才会被接受为区块链的新头。实际上,由于网络中压倒性的哈希率,单个矿工赢得 PoW 竞赛的机会可以忽略不计。因此,现实世界的区块链网络由代表矿工联盟的代理节点主导,这些节点被称为矿池。矿池作为任务调度器,将原像搜索任务划分为更小的子任务,并根据矿工的投入/报告哈希率将它们分配给矿池中的矿工。通过聚合许多矿工的哈希率,矿池赢得区块奖励的概率变得非常大。然后,单个矿工可以根据其在池中的哈希率份额来确保其少量但稳定的奖励份额。
在这篇论文中,我们研究了基于 PoW 的区块链网络中的矿池选择问题。我们认为个体矿工是有限理性的,矿池采用任意的挖掘策略。我们将网络中的池选择动态建模为演化博弈模型。我们关注哈希率和传播延迟对策略演化的影响,并研究了两个矿池情况下矿池选择动态的演化稳定性。
Section2-Problem Formulation
涉及参数
- $$N: 区块链网络中独立矿工数量$$
- $$M: 区块链网络中独立矿工形成的矿池数量$$
- $$\mathcal {M}:所有矿池的集合$$
- $$\omega _{i}: 矿池i要求每个独立矿工提供的哈希率$$
- $$\pmb {\omega }: 所有矿池要求每个独立矿工提供的哈希率集合$$
- $$x_{i}: 矿池i中矿工人数占总人数比例$$
- $$\mathbf {x}: 各个矿池中矿工人数占总人数比例的集合$$
- $${\Pr }^{\textrm {mine}}_{i}(\mathbf {x},\pmb {\omega }): 矿池i赢得挖矿竞赛的概率$$
- $$s: 区块大小$$
- $$\gamma: 网络规模相关参数$$
- $$c: 每个链路平均有效信道容量$$
- $$\tau _{p}(s): 大小为s的块的传输延迟时间$$
- $$\beta: 由网络规模和每个节点的平均验证速度共同决定的参数$$
- $$\tau _{v}(s): 验证大小为s的块所需的时间$$
- $${\Pr }^{\textrm {orphan}}(s): 孤立大小为 s 的有效块的概率$$
- $${\Pr }^{\textrm {win}}_{i}(\mathbf {x}, \pmb {\omega }, si): 矿池 i 最终赢得一个大小为si的区块的挖矿竞赛的概率是$$
- $$R: 代币发行的奖励$$
- $$\rho: 每单位数据大小的交易确认价格$$
- $$\rho s_{i}: 区块交易的手续费$$
- $$p: 在 T 期间维持单位哈希率的能源价格$$
- $$p\omega _{i}: 能量成本$$
- $$y_{i}(\mathbf {x}, \pmb {\omega }, s_{i}): 矿工在矿池 i 中的期望收益$$
A.利用POW机制进行挖矿的矿工收益计算
现假设有一个基于POW的区块链网络,其中有N个独立矿工,这些矿工自行组织成M个矿池,这些矿池的集合可以表示为$$\mathcal {M}={1, 2, \ldots, M}$$,我们假设解谜过程是抗ASIC的,换句话说,矿工使用通用计算单元进行哈希查询,并且具有大致相同的哈希效率,即每瓦特的哈希率。矿池i要求每个加入矿池的矿工提供一定的哈希率
$$\omega _{i}$$
$$\pmb {\omega }=[\omega _{1},\ldots, \omega _{M}]^{\top }$$
表示所有矿池要求每个独立矿工提供的哈希率集合,另外,让
$$\mathbf {x}=[x_{1},\ldots,x_{M}]^{\top }$$
表示矿池中矿工人数占总体矿工数的比例,即
$$\mathcal {X}=\left<!–swig1–> x_{i}=1}\right}$$
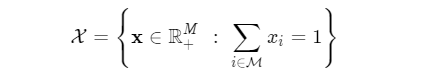
综上所述,矿池i赢得挖矿竞赛的概率为:
$${\Pr }^{\textrm {mine}}_{i}(\mathbf {x},\pmb {\omega })=\frac {\omega {i} x{i}}{\sum _{j=1}^{M}\omega {j} x{j}}$$
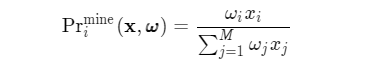
矿池 i 向所有P2P网络中的对等方广播一个成功开采的区块,以将其传播到整个网络。区块传播时间由每条链路上的传输延迟和每个中继节点的交易验证时间决定。对于大小为s的块,传输延迟可以建模为
$$\tau _{p}(s)=\frac {s}{\gamma c}$$
其中
$$\gamma$$
表示网络规模相关参数,c是每个链路的平均有效信道容量。同时,由于验证一笔交易需要固定的计算量,区块验证时间可以建模为线性函数
$$\tau _{v}(s)=\beta s$$
其中
$$\beta$$
是由网络规模和每个节点的平均验证速度共同决定的参数.然后,大小为 s 的块在网络中传播的平均时间为:
$$ \tau (s)=\tau _{p}(s)+\tau _{v}(s)=\frac {s}{\gamma c}+\beta s. $$
由于传播延迟而放弃(即孤立)有效候选块的发生率遵循泊松过程(补充),平均速率为 1/T,由网络维持为固定的平均挖掘速率。因此,孤立大小为 s 的有效块的概率为:
$${\Pr }^{\textrm {orphan}}(s)=1-e^{-\tau (s)/T}=1-e^{-\left({\frac {s}{\gamma c}+\beta s}\right) /T}.$$
所以,然后,矿池 i 最终赢得一个大小为
$$s_{i}$$
的区块的挖矿竞赛的概率是 ( 赢得竞赛的概率乘挖到的区块不被孤立的概率 ) :
$${\Pr }^{\textrm {win}}{i}(\mathbf {x}, \pmb {\omega }, s{i})=(1-{\Pr }^{\textrm {orphan}}(s))*{\Pr }^{\textrm {mine}}{i}(\mathbf {x},\pmb {\omega })=\frac {\omega {i} x{i}}{\sum {j=1}^{M}\omega {j} x{j}} e^{-\left({\frac {s{i}}{\gamma c}+\beta s{i}}\right)/T}.$$

一个区块的收益由固定的代币发行奖励和打包在新区块中的所有交易的交易费用组成。考虑到区块链用户为每笔交易支付固定费用并且交易记录具有相同的大小。令 R 表示代币发行奖励,
$$\rho$$
表示每单位数据大小的交易确认价格。然后,交易费用可以表示为
$$\rho s_{i}$$
由于哈希计算,矿工还必须考虑能源成本。让 p 表示在 T 期间维持单位哈希率的能源价格。能量成本可以表示为
$$p\omega _{i}$$
结合之前的讨论,矿工在矿池 i 中的期望收益可以表示为
$$y_{i}(\mathbf {x}, \pmb {\omega }, s_{i})=\frac {R+\rho s_{i}}{N x_{i}}\frac {\omega {i} x{i}}{\sum {j=1}^{M}\omega {j} x{j}} e^{-\left({\frac {s{i}}{\gamma c}+\beta s_{i}}\right)/T}-p\omega _{i}.\qquad $$

B.矿池选择过程中的演化博弈
考虑到每个矿工都是有限理性的,并且旨在最大化其个体的收益。所以我们可以将矿池选择过程中的演化博弈定义为一个四元组:
$$\mathcal {G}=\langle \mathcal {N}, \mathcal {M}, \mathbf {x}, {y_{i}(\mathbf {x}, \pmb {\omega }, s_{i})}_{i\in \mathcal {M}} \rangle$$
- $$其中\mathcal {N}表示个体矿工人数,并且\vert \mathcal {N}\vert =N$$
- $$\mathcal {M}={1, 2, \ldots, M}表示所有矿池的集合$$
- $$\mathbf {x}\in \mathcal {X}表示人口状态向量$$
- $${y_{i}(\mathbf {x}, \pmb {\omega }, s_{i})}_{i\in \mathcal {M}}表示每个矿池中单个矿工收益的集合$$
最后,根据成对比例模仿协议,我们完成了矿池选择过程中的演化博弈过程
1 | /* |
转换概率公式:
$$\rho {i,j}=x{j}\max (y_{j}(\mathbf {x}, \pmb {\omega }, s_{j}) - y_{i}(\mathbf {x}, \pmb {\omega }, s_{i}), 0)$$
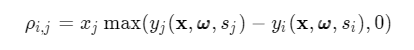
仿真过程
补充知识
挖掘策略
挖掘策略:指矿工在解谜过程以及最后公布区块阶段采取的相应策略,旨在通过合法的方式增大自己的收益,常见的挖掘策略有自私挖掘与合作挖掘,从而还衍生出了智能矿工的概念(不断动态分析各个矿池的数据,可以动态获到当前收益最高的矿池,选择收益最高的矿池)
自私挖掘:自私挖掘主要通过扣留区块,拖延公布区块的时间来达成。- 自私挖矿的目的不是破坏加密货币的区块链网络,而是获得更大利润。
这种攻击主要由矿工发起。我们以比特币区块链作为例子。简单地说,攻击者挖到新区块后藏起来不公布,其他诚实矿工因为不知道新区块的存在,还是继续在旧区块基础上挖矿。等到攻击者挖到第二枚区块后便会同时公布手中藏着的两枚区块,这时,区块链分叉就出现了。只要攻击者比诚实矿工多挖一枚区块,攻击者所在的分叉就是最长链:根据比特币的共识机制,矿工只在最长链后面挖矿。因此,原本诚实矿工们所在的那条链,因为比攻击者的分叉短,便作废了。此时此刻,攻击者因为挖到了两枚新区块而获得相应收益;而诚实矿工的分叉被废弃,他们什么也得不到。
这种攻击的前提是对于算力(即挖矿速度)的比拼。如同刚才提到的,面对区块链出现分叉情况时(这里的分叉不是日常所说改变共识原则的硬分叉或软分叉,而是在共识原则不变前提下的分叉),最长的那一条链被视作合法链。如果自私挖矿攻击者能够迅速让原本的长链变成短链(即在短时间内发布自己挖到的两枚或多枚区块,让自己所在的区块链分叉变成最长链),那么所有诚实守法的矿工所做的努力都白费了。
抗ASIC
ASIC是专用继承电路的缩写,是为特定目的而生产的微芯片,在加密货币领域,ASIC最常用于计算密码难题,特别是用于挖矿过程。
顾名思义,抗ASIC是指能够有效抗击ASIC的算法,常见的具有抗ASIC性的货币有以太坊等
孤立块
孤立块的出现是由于意外分叉,意外分叉即两个或以上的矿工在几乎相同的时间成功挖到区块,此时原来的区块链便会产生分叉,而收到不同区块的两组矿工便会在两条分叉的链上继续挖矿,直至其中一组矿工首先挖到下一枚区块,生成了更长链,此时网络中的矿工便会舍弃原来较短的链上的最后一枚区块,转而相信最长链的数据,分叉也随之消失,而被舍弃的那枚区块,就叫做孤立块。





