Arithmetic Progression Graphs
算术级数图(Arithmetic Progression Graphs,简称 APG),是一类特殊的加权图模型,其核心特征来源于等差数列(Arithmetic Progression)。
等差数列是一组数列,其中任意两个相邻元素之间的差值恒定,该固定差值称为公差。APG 将这一数列结构引入图论中,用于约束顶点权重与边权之间的关系。
一、APG 的基本定义
在 Arithmetic Progression Graph 中:
- 图中所有顶点的权重按某一固定顺序构成一个等差数列
- 每个顶点关联的所有边的权重之和,必须严格等于该顶点的权重
形式化描述如下:
- 设图
- 顶点集合
- 顶点权重满足
- 对任意顶点 ,其所有关联边权之和满足
其中 表示与顶点 相连的所有边集合。
二、示例说明
下图给出了一个 Arithmetic Progression Graph 的示意结构,其中顶点权重呈等差递增,同时每个顶点的入边与出边权重之和严格匹配其顶点权重:
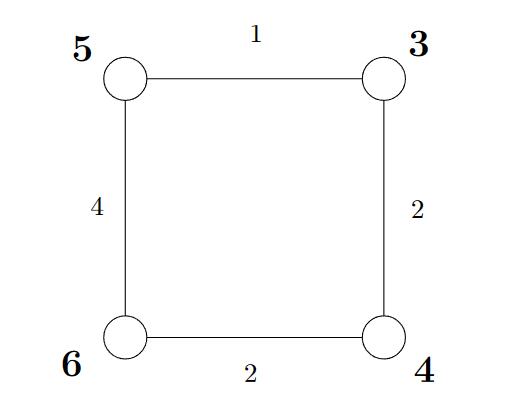
该示例直观体现了 APG 的两个核心约束:
- 顶点权重具有全局的等差结构
- 边权分配在局部上满足“守恒”条件
三、APG 的一些已知性质
在已有研究与推导中,Arithmetic Progression Graph 具有如下典型特性:

这些性质通常涉及:
- 顶点度数与权重分布之间的关系
- 边权解的存在性与唯一性
- 图的连通性对 APG 可行性的影响
四、APG 判定问题
问题描述
给定一幅加权图,其所有顶点权重已知且构成等差数列,如何判断该图是否可以被视为一个 Arithmetic Progression Graph?
本质分析
该问题的核心并不在于顶点权重本身,而在于:
是否存在一组边权分配,使得每个顶点相邻边的权重之和恰好等于该顶点的权重。
换言之,这是一个关于**边权可行性(feasible edge-weight assignment)**的问题,常可转化为:
- 线性方程组是否存在非负解
- 或网络流 / 可行流问题
- 或图结构约束下的加权平衡问题
示意图
下图展示了一个用于 APG 判定的典型结构示例:
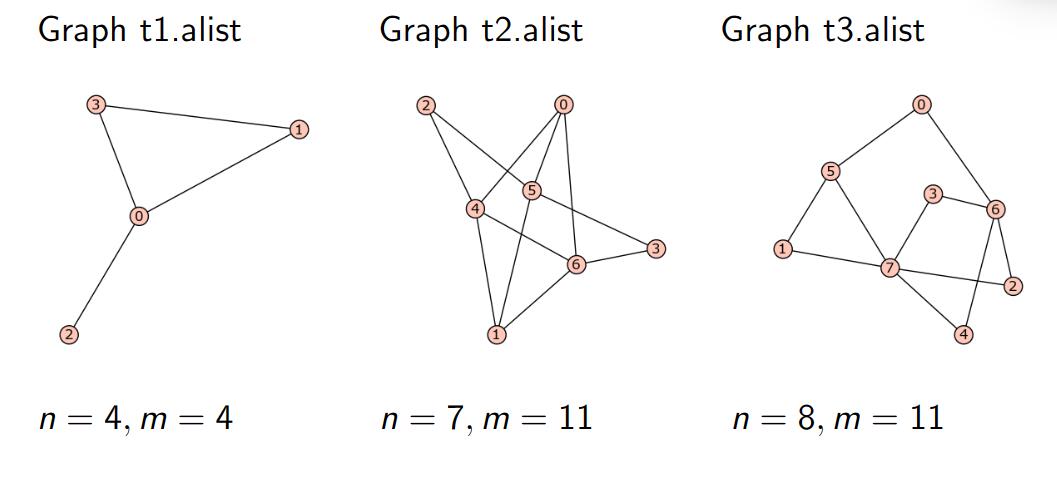
五、小结
Arithmetic Progression Graph 将等差数列与图论结构相结合,形成了一类具有明确数值约束的加权图模型。其研究重点主要集中在:
- 边权分配的存在性
- 图结构对可行解的影响
- 以及相关算法判定问题